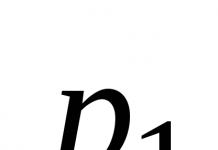Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Линейные дифференциальные уравнения второго порядка» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)

Горки, 2013

Линейные дифференциальные уравнения

второго порядка с постоянными коэффициентами

1. Линейные однородные дифференциальные уравнения

Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

т.е. уравнение, которое содержит искомую функцию и её производные только в первой степени и не содержит их произведений. В этом уравнении и
- некоторые числа, а функция
задана на некотором интервале
.

Если
на интервале
, то уравнение (1) примет вид

, (2)

и называется линейным однородным . В противном случае уравнение (1) называется линейным неоднородным .

Рассмотрим комплексную функцию

, (3)

где
и
- действительные функции. Если функция (3) является комплексным решением уравнения (2), то и действительная часть
, и мнимая часть
решения
в отдельности являются решениями этого же однородного уравнения. Таким образом, всякое комплексное решение уравнения (2) порождает два действительных решения этого уравнения.

Решения однородного линейного уравнения обладают свойствами:

Если есть решение уравнения (2), то и функция
, где С – произвольная постоянная, также будет решением уравнения (2);

Если и есть решения уравнения (2), то и функция
также будет решением уравнения (2);

Если и есть решения уравнения (2), то их линейная комбинация
также будет решением уравнения (2), где и
– произвольные постоянные.

Функции
и
называются линейно зависимыми на интервале
, если существуют такие числа и
, не равные нулю одновременно, что на этом интервале выполняется равенство

Если равенство (4) имеет место только тогда, когда
и
, то функции
и
называются линейно независимыми на интервале
.

Пример 1 . Функции
и
линейно зависимы, так как
на всей числовой прямой. В этом примере
.

Пример 2 . Функции
и
линейно независимы на любом интервале, т. к. равенство
возможно лишь в случае, когда и
, и
.

1. Построение общего решения линейного однородного

уравнения

Для того, чтобы найти общее решение уравнения (2), нужно найти два его линейно независимых решения и . Линейная комбинация этих решений
, где и
– произвольные постоянные, и даст общее решение линейного однородного уравнения.

Линейно независимые решения уравнения (2) будем искать в виде

, (5)

где – некоторое число. Тогда
,
. Подставим эти выражения в уравнение (2):

Или
.

Так как
, то
. Таким образом, функция
будет решением уравнения (2), если будет удовлетворять уравнению

. (6)

Уравнение (6) называется характеристическим уравнением для уравнения (2). Это уравнение является алгебраическим квадратным уравнением.

Пусть и есть корни этого уравнения. Они могут быть или действительными и различными, или комплексными, или действительными и равными. Рассмотрим эти случаи.

Пусть корни и характеристического уравнения действительные и различны. Тогда решениями уравнения (2) будут функции
и
. Эти решения линейно независимы, так как равенство
может выполняться лишь тогда, когда и
, и
. Поэтому общее решение уравнения (2) имеет вид

,

где и
- произвольные постоянные.

Пример 3
.

Решение . Характеристическим уравнением для данного дифференциального будет
. Решив это квадратное уравнение, найдём его корни
и
. Функции
и
являются решениями дифференциального уравнения. Общее решение этого уравнения имеет вид
.

Комплексным числом называется выражение вида
, где и - действительные числа, а
называется мнимой единицей. Если
, то число
называется чисто мнимым. Если же
, то число
отождествляется с действительным числом .

Число называется действительной частью комплексного числа, а - мнимой частью. Если два комплексных числа отличаются друг от друга только знаком мнимой части, то они зазываются сопряжёнными:
,
.

Пример 4 . Решить квадратное уравнение
.

Решение . Дискриминант уравнения
. Тогда . Аналогично,
. Таким образом, данное квадратное уравнение имеет сопряжённые комплексные корни.

Пусть корни характеристического уравнения комплексные, т.е.
,
, где
. Решения уравнения (2) можно записать в виде
,
или
,
. По формулам Эйлера

,
.

Тогда , . Как известно, если комплексная функция является решением линейного однородного уравнения, то решениями этого уравнения являются и действительная, и мнимая части этой функции. Таким образом, решениями уравнения (2) будут функции
и
. Так как равенство

может выполняться только в том случае, если
и
, то эти решения линейно независимы. Следовательно, общее решение уравнения (2) имеет вид

где и
- произвольные постоянные.

Пример 5 . Найти общее решение дифференциального уравнения
.

Решение . Уравнение
является характеристическим для данного дифференциального. Решим его и получим комплексные корни
,
. Функции
и
являются линейно независимыми решениями дифференциального уравнения. Общее решение этого уравнения имеет вид .

Пусть корни характеристического уравнения действительные и равные, т.е.
. Тогда решениями уравнения (2) являются функции
и
. Эти решения линейно независимы, так как выражение может быть тождественно равным нулю только тогда, когда
и
. Следовательно, общее решение уравнения (2) имеет вид
.

Пример 6 . Найти общее решение дифференциального уравнения
.

Решение . Характеристическое уравнение
имеет равные корни
. В этом случае линейно независимыми решениями дифференциального уравнения являются функции
и
. Общее решение имеет вид
.

§ 9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Определение ЛОДУ второго порядка с постоянными коэффициентами

Характеристическое уравнение:

Случай1. Дискриминант больше нуля

Случай2. Дискриминант равен нулю

Случай3. Дискриминант меньше нуля

Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами

§ 10. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Определение ЛНДУ второго порядка с постоянными коэффициентами

Метод вариации постоянных

Метод решения ЛНДУ со специальной правой частью

Теорема о структуре общего решения ЛНДУ

1. Функция r (x ) – многочлен степени т

2. Функция r (x ) – произведение числа на показательную функцию

3. Функция r (x ) – сумма тригонометрических функций

Алгоритм нахождения общего решения ЛНДУ со специальной правой частью

Приложение

§ 9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Дифференциальное уравнение второго порядка называется линейным однородным дифференциальным уравнением (ЛОДУ) с постоянными коэффициентами , если оно имеет вид:

где p и q

Для нахождения общего решения ЛОДУ достаточно найти два его различных частных решения и . Тогда общее решение ЛОДУ будет иметь вид

где С 1 и С

Леонард Эйлер предложил искать частные решения ЛОДУ в виде

где k – некоторое число.

Дифференцируя эту функцию два раза и подставляя выражения для у , у" и у" в уравнение , получим:

Полученное уравнение называется характеристическим уравнением ЛОДУ. Для его составления достаточно в исходном уравнении заменить у" , у" и у соответственно на k 2 , k и 1:

Решив характеристическое уравнение, т.е. найдя корни k 1 и k 2 ,мы найдем и частные решения исходного ЛОДУ.

Характеристическое уравнение есть квадратное уравнение, его корни находятся через дискриминант

При этом возможны следующие три случая .

Случай 1 . Дискриминант больше нуля , следовательно, корни k 1 и k 2 действительные и различные:

k 1 ¹ k 2

где С 1 и С 2 – произвольные независимые постоянные.

Случай 2 . Дискриминант равен нулю , следовательно, корни k 1 и k 2 действительные и равные:

k 1 = k 2 = k

В этом случае общее решение ЛОДУ имеет вид

где С 1 и С 2 – произвольные независимые постоянные.

Случай 3 . Дискриминант меньше нуля . В этом случае уравнение не имеет действительных корней:

Корней нет.

В этом случае общее решение ЛОДУ имеет вид

где С 1 и С 2 – произвольные независимые постоянные,

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами сводится к нахождению корней характеристического уравнения и использованию формул общего решения уравнения (не прибегая к вычислению интегралов).

Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами :

1. Привести уравнение к виду , где p и q – некоторые действительные числа.

2. Составить характеристическое уравнение .

3. Найти дискриминант характеристического уравнения.

4. Используя формулы (см. Таблицу 1), в зависимости от знака дискриминанта записать общее решение.

Таблица 1

Таблица возможных общих решений

Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид

где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.

1) Если корни характеристического уравнения — различные действительные числа:

то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

2) Если корни характеристического уравнения — равные действительные числа

(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть

3) Если корни характеристического уравнения — комплексные числа

(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде

Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Найти общие решения однородных дифференциальных уравнений второго порядка:

Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.

Отсюда, общее решение этого однородного ДУ 2-го порядка есть

Составим и решим характеристическое уравнение:

Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:

В этом случае характеристическое уравнение

Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь

Характеристическое уравнение

Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как

Характеристическое уравнение здесь

Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.

Общее решение этого однородного дифференциального уравнения второго порядка имеет вид

Характеристическое уравнение

Отсюда находим общее решение данного диф. уравнения:

Примеры для самопроверки.

Линейное дифференциальное уравнение (ЛДУ) 2-го порядка имеет следующий вид:

где , , и – заданные функции, непрерывные на том промежутке, на котором ищется решение. Предполагая, что a 0 (x) ≠ 0, поделим (2.1) на и, после введения новых обозначений для коэффициентов, запишем уравнение в виде:

Примем без доказательства, что (2.2) имеет на некотором промежутке единственное решение, удовлетворяющее любым начальным условиям , , если на рассматриваемом промежутке функции , и непрерывны. Если , то уравнение (2.2) называется однородным, и уравнение (2.2) называется неоднородным в противном случае.

Рассмотрим свойства решений лоду 2-го порядка.

Определение. Линейной комбинацией функций называется выражение , где – произвольные числа.

Теорема. Если и – решение лоду

то их линейная комбинация также будет решением этого уравнения.

Доказательство.

Поставим выражение в (2.3) и покажем, что в результате получается тождество:

Перегруппируем слагаемые:

Поскольку функции и являются решениями уравнения (2.3), то каждая из скобок в последнем уравнении тождественно равна нулю, что и требовалось доказать.

Следствие 1. Из доказанной теоремы вытекает при , что если – решение уравнения (2.3), то тоже есть решение этого уравнения.

Следствие 2. Полагая , видим, что сумма двух решений лоду также является решением этого уравнения.

Замечание. Доказанное в теореме свойство решений остается справедливым для лоду любого порядка.

§3. Определитель Вронского.

Определение. Система функций называется линейно независимой на некотором промежутке, если ни одна из этих функций не представляется в виде линейной комбинации всех остальных.

В случае двух функций это означает, что , т.е. . Последнее условие можно переписать в виде или . Стоящий в числителе этого выражения определитель называется определителем Вронского для функций и . Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю.

Пусть – определитель Вронского для линейно независимых решений и уравнения (2.3). Убедимся подстановкой, что функция удовлетворяет уравнению . (3.1)

Действительно, . Поскольку функции и удовлетворяют уравнению (2.3), то , т.е. – решение уравнения (3.1). Найдем это решение: ; . Откуда , . , , .

В правой части этой формулы надо взять знак плюс, так как только в этом случае при получается тождество. Таким образом,

(3.2)

Это формула называется формулой Лиувилля. Выше было показано, что определитель Вронского для линейно независимых функций не может быть тождественно равен нулю. Следовательно, существует такая точка , в которой определитель для линейно независимых решений уравнения (2.3) отличен от нуля. Тогда из формулы Лиувилля следует, что функция будет отлична от нуля при всех значениях из рассматриваемого промежутка, поскольку при любом значении оба множителя в правой части формулы (3.2) отличны от нуля.

§4. Структура общего решения лоду 2-го порядка.

Теорема. Если и – линейно независимые решения уравнения (2.3), то их линейная комбинация , где и – произвольные постоянные, будет общим решением этого уравнения.

Доказательство.

То, что есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение будет общим , т.е. надо показать, что при любых начальных условиях , можно выбрать произвольные постоянные и так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:

Постоянные и из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы есть значение определителя Вронского для линейно независимых решений лоду при :

,

а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля. Теорема доказана.

Пример. Доказать, что функция , где и – произвольные постоянные, является общим решением лоду .

Решение.

Легко убедиться подстановкой, что функции и удовлетворяют данному уравнению. Эти функции являются линейно независимыми, так как . Поэтому согласно теореме о структуре общего решения лоду 2-го порядка является общим решением данного уравнения.